• Benefits
• Kingsland Camp
• Clock

The duodecimal system (also known as base 12 or dozenal) is a positional notation numeral system using twelve as its base.

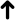Benefits

A base 12 system is better than the decimal system both mathematically and for other practical purposes. Indeed 2,3,4,6 are divisors of 12, which facilitates the fractionalization. Compared to the 2 and 5 divisors of the decimal system, the duodecimal system offers more possibilities.

Counting in tens is a biological accident. There is no doubt that we would have adopted a base 12 system if we had been born with so many fingers, and everything would have been much simpler!

There is nevertheless an effective way to count on one’s fingers in base 12: count the phalanges of the hand by omitting those of the thumb (which is used to count the phalanges of other fingers):

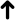Kingsland Camp

On base 12, the 10 digits from 0 to 9 are used, followed by the letters A and B, respectively for 10 and 11. (see here), but adding two new digits is a good opportunity to create a new numerical system with much more consistent symbols.

Kingsland Camp described more than one “ideal” set of numerals in his article “Number symbols” (The Duodecimal Bulletin, Vol.2, n°1, page 16).
Here we propose to adopt this system, modifying the symbols’ value so that the 6 is the cipher on the top of a dial:

The symmetrical geometries of his numerals were intended to more purely convey the digit they represent, by their rotational orientations:

• Halves are represented by { , }, circles with vertical strokes through their centers.
• Odd quarters by { , }, circles with strokes left or right. {0, 3, 6, 9}

The numerals representing the range of quarters { 0, 3, 6, 9 } can be read like clock faces: { , , , }.

• Camp’s notation expresses thirds by { , }
  and the sequence of sixths by { , , , , , }.

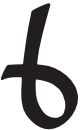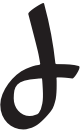Thus any numeral representing a sixth of a dozen not already covered by the quarters appears as a “fish” shaped symbol.

• Camp’s notation also treats the other odd numbers { 1, 5, 7, B } in a way that accentuates them, a sharp angular numeral opening up to the numeral’s position on a standard clock face: { , , , }

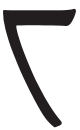Clock

Here is an ideal proposal for a duodecimal clock: https://clock.dozenal.ca/clock/diurnal_1

The little needle goes around in one day. It is midnight when it is on 0, and noon when it points to 6 (analogous to the position of the sun at this time of day). Each needle spins 12 times faster than the previous shorter one, so each needle spins 1/12th of a revolution at each complete turn of the next needle.

It is very easy to read the time: just read the number to which the hands point. At noon, it’s 600. This avoids breaking your head if you want to calculate the elapsed time between 11:31:40 and 16:03:20, for example.
16:03:20 – 11:31:40 = 4:31:40 ➜ 804 – 592 = 232